Svet u kome živimo pun je obrazaca koji se mogu opisati uz pomoć matematike. Duga na nebu, rečni meandri, senke u prostoru, paukova mreža, saće, šare na životinjkom krznu, samo su neke od prirodnih pojava u kojima se pronalaze matematički principi. Matematika je svuda oko nas i sve je broj. Izložba "Matematika i priroda" prvi put je prikazana u okviru manifestacije "Maj mesec matematike", koji su Centar za promociju nauke i Matematički institut SANU realizovali u Beogradu 2013. godine.
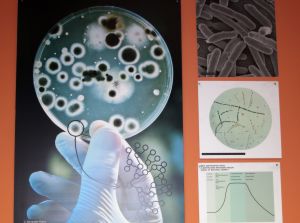
Rast bakterija
Da li znate da su bakterije najbrojniji organizmi na našoj planeti? Najveći broj bakterijskih vrsta razmnožava se binarnom deobom (fisijom) pri kojoj se jednaćelija podeli na dve. Ako se deoba dešava svakih sat vremena i za početak imamo jednu bakteriju, nakon samo jednog dana biće ih preko 16 miliona! Rast bakterija naziva se eksponencijalni rast i može se opisati formulom:
Simetrija
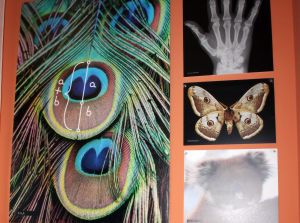
Kada se pogledate u ogledalo, videćete jedan od najlepših primera bilateralne simetrije! Simetrični oblici su oni koji imaju ravan, osu i centar simetrije. Sigurno ste već primetili da postoje i organizmi koji nisu bilateralno simetrični. Mnogi od njih imaju radijalnu (zračnu) simetriju i često su svernog ili cilindričnog oblika.
Paralelne linije
Osvrnite se oko sebe i pogledajte paživo – videćete primere paralelnosti skoro svuda, i u biljnom i u životinjskom svetu. Paralelnost u geometriji predstavlja odnos između dva geometrijska tela. Dve prave su paralelne ako se nalaze u jednoj ravni i ne seku se.
Geometrijski oblici
Da li ste znali da su pčele odlični matematičari? Izabrali su baš šetougao za model građe saća, jer se tako postiže najbolje iskorišćenje materijala i prostora. Još jedna geometriska forma veoma zastupljena u prirodi jeste lopta, telo ograničeno sverom koju matematičari često nazivaju "savršenom geometrijskom telom".
Zlatni presek
Iznenadićete se koliko je lako uočiti u prirodi primere zlatnog preseka – odnos dve veličine koji zadovoljava jednostavno pravilo: odnos njihovog zbira i veće veličine jednak je odnosu veće veličine prema manjoj. Ovaj specifičan odnos često su kroz istoriju nazivali "univerzalnim zakonom".
Fibonačijev niz
Latice brojnih vrsta cveća, listove drveća, uragane, galaksije, seme suncokreta i ljudsko uho povezuje isti princip – svi imaju spiralni oblik oji se skoro savršeno poklapa sa "zlatnom spiralom" nastalom tzv. Fibonačijevom nizom:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Uočićete da je svaki sledeći broj jednak zbiru prethodna dva.
Fraktali
Šta je to zajedničko za snežne pahulje, munje, neke morske obale, karfiol, grananje drveća i neurona i planinske vence? Sve su to sjajni primeri tzv. prirodnih fraktala. Fraktal je geometrijski lik koji se može razložiti na manje delove tako da je svaki od njih, makar približno, umanjena kopija celine. Obično se kaže da je fraktal sam sebi sličan.
Pruge
Mnogi smatraju da je priroda vešta umetnica. Ali malo je poznato da gotovo nestvarno lepe i raznovsne prirodne pruge i šare mogu da budu opisane matematičkim formulama.
Pege i šare
Alan Tjuring došao je na genijalnu ideju da jednačinama opiše nastanak raznovrsnih šara na koži, perju i krznu životinja. Zamislite embrion sa dve vrste hemijskih jedinjenja u sebi (aktivator i inhibitor) koja zajedničkim dejstvom na pigmente stvaraju mnogobrojne šare. Od promene koncentracije tih jedinjenja tokom vremena zavisi izgled pega leoparda. Matematičari to opisuju ovako:
