A világ, amelyben élünk tele van olyan mintákkal, melyeket körülírhatunk a matematika segítségével. A szivárvány, a folyókanyarok, az árnyékok, a pókháló, a méhsejt, a csíkok az állatok bundáján csak néhány olyan természetbeli jelenség, amelyekben fellelhetők a matematikai szabályszerűségek. A Matematika és a természet elnevezésű kiállítás a Május, a matematika hónapja rendezvény keretein belül került először bemutatásra, amelyre a Tudománynépszerűsítő Központ és a Szerb Tudományos és Művészeti Akadémia Matematikai Intézete szervezésében került sor Belgrádban, 2013-ban.
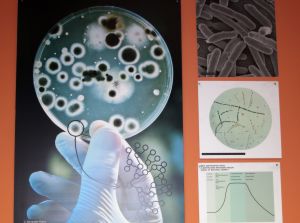
A baktériumok növekedése
Tudtátok-e, hogy a baktériumok a legnépesebb organizmus-fajta a bolygónkon? A baktériumok fajtáinak legtöbbje bináris osztódással (fisszió) szaporodik, melynek alkalmával egy sejtből kettő lesz. Ha az osztódás óránként ismétlődik, és kezdetben egy baktériumunk volt, mindössze egyetlen nap elteltével a számuk 16 millió felett lesz! A baktériumok növekedését ekszponenciális növekedésnek hívjuk, és a következő képlettel írható le:
Szimmetria
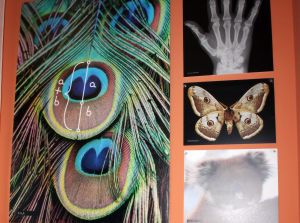
Ha belenéztek a tükörbe, megláthatjátok a bilaterális (kétoldali) szimmetria egyik legszebb példáját! A szimmetrikus alakzatoknak van síkja, tengelye és szimmetria-központja. Több esetben rendelkeznek radiális (sugár) szimmetriával és sokszor gömb vagy henger alakúak.
Párhuzamos vonalak
Nézzetek körül figyelmesen – szinte mindenhol felfedezhetitek a párhuzamosság példáit a növény- és állatvilágban egyaránt. A mértanban a párhuzamosság két mértani alakzat viszonyát jelenti. Két egyenes akkor párhuzamos, ha egy síkban vannak, és nem metszik egymást.
Mértani alakzatok
Tudtátok, hogy a méhek kiváló matematikusok? Éppen a hatszöget választották ki méhsejtjeik kiépítéséhez, mert így a legoptimálisabb az anyag és a tér felhasználása. A másik, igen gyakori mértani alakzat a természetben a gömb, az a gömbfelülettel határolt alakzat, amelyet a matematikusok gyakran neveznek a "legtökéletesebb mértani alakzatnak".
Aranymetszés
Meg fogtok lepődni, milyen egyszerű fellelni a természetben az aranymetszés példáit – két rész egymáshoz való viszonyát, mely a következőképpen írható le: két rész az aranymetszés szerint aránylik egymáshoz, ha az egész úgy aránylik a nagyobbik részhez, ahogy a nagyobbik rész a kisebbik részhez. Ezt a specifikus viszonyt gyakran nevezték a történelem folyamán "univerzális törvénynek".
Fibonacci sorozat
Számos virágfaj szirmai, a falevelek, hurrikánok, galaxisok, napraforgószemek és az emberi fül közös vonása, hogy mind spirál alakú, amely görbe szinte a tökéletességig megfelel az "arany spirálnak", amely az ún. Fibonacci sorozat nyomán keletkezik:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Megfigyelhetitek, hogy a számsorban minden szám az előtte lévő két szám összege.
Fraktálok
Mi az, ami közös a hópelyhekben, a villámokban, a tengerpart egyes részeiben, a karfiolban, a fák ágainak elrendeződésében, a neuronokban és a hegyláncokban? Mindannyian kiváló példái a természetes fraktáloknak. A fraktálok olyan mértani alakzatok, amelyek kisebb részekre bonthatók, és ezek a kisebb részek – ha csak megközelítőleg is, de – a teljes alakzat másolatai kicsiben. Általában azt mondják, hogy a fraktálok önmagukhoz hasonlóak.
Csíkok
Sokan gondolják azt, hogy a természet nagyszerű művész. Az már kevésbé ismert tény, hogy szinte hihetetlenül szép és változatos természetes csík és mintázat leírható matematikai egyenletekkel.
Pöttyök és minták
Alan Turingnak támadt az a brilliáns ötlete, hogy matematikai úton, képletekkel fejezze ki az egyes mintázatok megjelenését a bőrön, a tollazaton és az állatok bundáján. Képzeljetek el egy embriót kétféle kémiai vegyülettel a testében (aktivátorral és inhibitorral), amelyek a pigmentekre gyakorolt együttes hatásukkal számos mintázatot hoznak létre. Az említett vegyületek koncentrációjának függvényében alakulnak ki idővel a leopárd pöttyei. A matematikusok ezt a következőképpen írják le:
